有趣的文章总是使人更易理解~——
Note:阅读本文需要有KMP算法基础,如果你不知道什么是KMP,请看这里:
http://www.matrix67.com/blog/article.asp?id=146 (Matrix67大牛写的)
AC自动机是用来处理多串匹配问题的,即给你很多串,再给你一篇文章,让你在文章中找这些串是否出现过,在哪出现。也许你考虑过AC自动机名字的含义,我也有过同样的想法。你现在已经知道KMP了,他之所以叫做KMP,是因为这个算法是由Knuth、Morris、Pratt三个提出来的,取了这三个人的名字的头一个字母。那么AC自动机也是同样的,他是Aho-Corasick。所以不要再YY地认为AC自动机是AC(cept)自动机,虽然他确实能帮你AC一点题目。
。。。扯远了。。。
要学会AC自动机,我们必须知道什么是Trie,即字母树。如果你会了,请跳过这一段
Trie是由字母组成的。
先看张图:
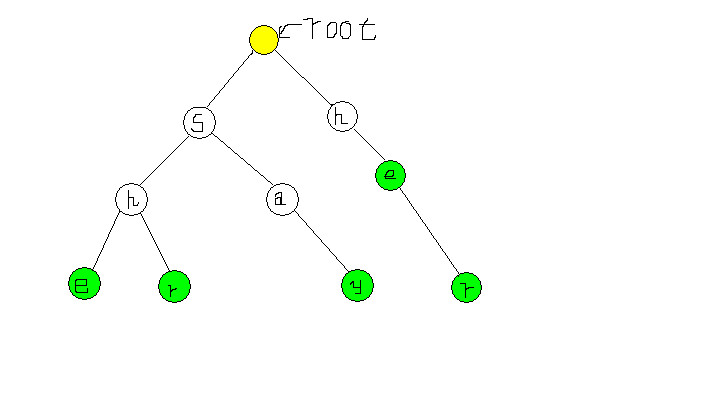
这就是一棵Trie树。用绿色标出的点表示一个单词的末尾(为什么这样表示?看下去就知道了)。树上一条从root到绿色节点的路径上的字母,组成了一个“单词”。
/* 也许你看了这一段,就知道如何构建Trie了,那请跳过以下几段。*/
那么如何来构建一棵Trie呢?就让我从一棵空树开始,一步步来构建他。
一开始,我们有一个root:
现在,插入第一个单词,she。这就相当于在树中插入一条链。过程很简单。插完以后,我们在最后一个字母’e’上加一个绿色标记,结果如图:
再来一个单词,shr(什么词?…..右位移啊)。由于root下已经有’s’了,我们就不重复插入了,同理,由于’s’下有’h’了,我们也略过他,直接在’h’下插入’r’,并把’r’标为绿色。结果如图:
按同样的方法,我们继续把余下的元素插进树中。
最后结果:
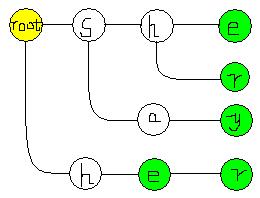
也就是这样:
好了,现在我们已经有一棵Trie了,但这还不够,我们还要在Trie上引入一个很强大的东西:失败指针或者说shift数组或者说Next函数 …..你爱怎么叫怎么叫吧,反正就是KMP的精华所在,这也是我为什么叫你看KMP的原因。
KMP中我们用两个指针i和j分别表示,A[i-j+ 1..i]与B[1..j]完全相等。也就是说,i是不断增加的,随着i的增加j相应地变化,且j满足以A[i]结尾的长度为j的字符串正好匹配B串的前 j个字符,当A[i+1]<>B[j+1],KMP的策略是调整j的位置(减小j值)使得A[i-j+1..i]与B[1..j]保持匹配且新的B[j+1]恰好与A[i+1]匹配(从而使得i和j能继续增加)。
Trie树上的失败指针与此类似。
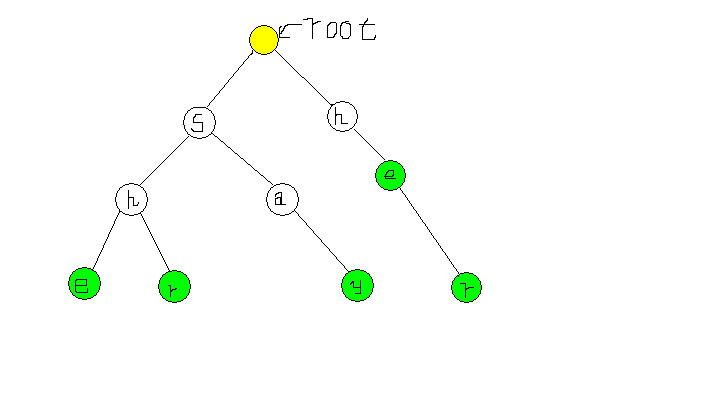
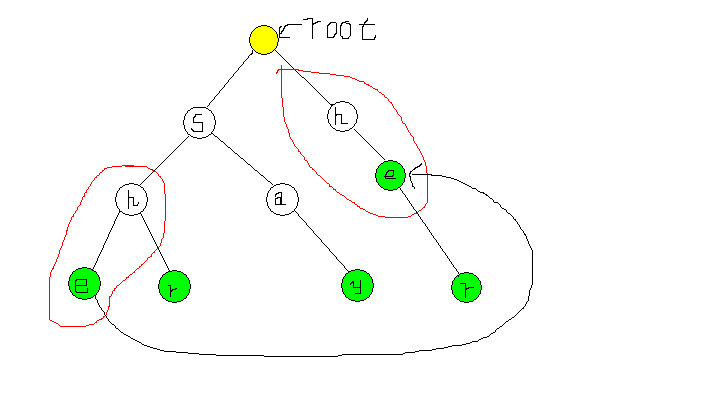
假设有一个节点k,他的失败指针指向j。那么k,j满足这个性质:设root到j的距离为n,则从k之上的第n个节点到k所组成的长度为n的单词,与从root到j所组成的单词相同。
比如图中she中的’e’的失败指针就应该指向her中的’e’。因为:
那么我们要怎样构建这个东西呢?其实我们可以用一个简单的BFS搞定这一切。
对于每个节点,我们可以这样处理:设这个节点上的字母为C,沿着他父亲的失败指针走,直到走到一个节点,他的儿子中也有字母为C的节点。然后把当前节点的失败指针指向那个字目也为C的儿子。如果一直走到了root都没找到,那就把失败指针指向root
最开始,我们把root加入队列(root的失败指针显然指向自己),这以后我们每处理一个点,就把它的所有儿子加入队列,直到搞完。
至于为什么这样就搞的定,我们讲下去就知道了。
好了,现在我们有了一棵带失败指针的Trie了,而我的文章也破千字了,接下来,我们就要讲AC自动机是怎么工作的了。
AC自动机是个多串匹配,也就是说会有很多串让你查找,我们先把这些串弄成一棵Trie,再搞一下失败指针,然后我们就可以开始AC自动机了。
一开始,Trie中有一个指针t1指向root,待匹配串(也就是“文章”)中有一个指针t2指向串头。
接下来的操作和KMP很相似:如果t2指向的字母,是Trie树中,t1指向的节点的儿子,那么t2+1,t1改为那个儿子的编号,否则t1顺这当前节点的失败指针向上找,直到t2是t1的一个儿子,或者t1指向根。如果t1路过了一个绿色的点,那么以这个点结尾的单词就算出现过了。或者如果t1所在的点可以顺着失败指针走到一个绿色点,那么以那个绿点结尾的单词就算出现过了。
我们现在回过来讲讲失败指针。实际上找失败指针的过程,是一个自我匹配的过程。
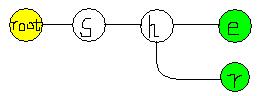
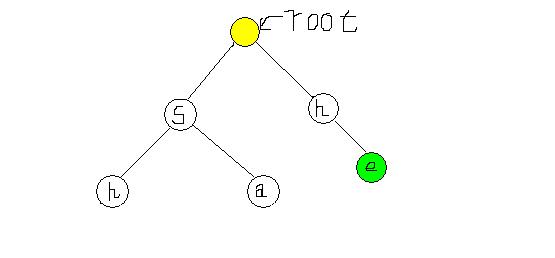
如图,现在假定我们确定了深度小于2(root深度为1)的所有点的失败指针,现在要确定e。这就相当于我们有了这样一颗Trie:
而文章为’she’,要查找’e’在哪里出现。我们接着匹配’say’,那’y’的失败指针就确定了。
好好想想。前面讲的BFS其实就是自我匹配的过程,这也是和KMP很相似的。
好了,就写到这吧,有不明白可以留言或发邮件给我(drdarkraven@gmail.com)
DarkRaven原创
看了以上的文章,应该对AC自动机有很好的了解了吧~~关于本题的技巧总结:
1、BFS进行自我匹配
2、-1表示无法匹配,0表示匹配到根
3、KMP思想在字典树上的完美应用
4、使用gets提速
以下是我实现的代码,还可以继续优化(代码已修正).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 | #include<iostream>#include<queue>using namespace std;struct node{ int f; int next[26]; int fall; void init(){memset(next,-1,sizeof(next));fall=-1,f=0;}}s[2000000];int p;char a[1000005];inline void preprocess(){s[p=0].init();s[0].fall=-1;}inline void insert(){ int ind=0; int i; for(i=0;a[i];++i) { int x=a[i]-'a'; if(s[ind].next[x]==-1) { s[++p].init(); s[ind].next[x]=p; } ind=s[ind].next[x]; } ++s[ind].f;}inline int find(){ int root=0; int i=0; int ct=0; int p=root; while(a[i]) { int ind=a[i]-'a'; while (p!=root&&s[p].next[ind]==-1) { p=s[p].fall; } p=s[p].next[ind]; if (p==-1) { p=root; } int tp=p; while (tp!=root&&s[tp].f!=-1) { ct+=s[tp].f; s[tp].f=-1; tp=s[tp].fall; } ++i; } return ct; }inline void KMP(){ int root=0; s[root].fall=-1; queue<int> q; q.push(root); while (!q.empty()) { int t=q.front(); q.pop(); int i; for (i=0;i<26;++i) { int ind=s[t].next[i]; if(ind!=-1) { if (t==root) { s[ind].fall=root; } else { int p=s[t].fall; while (p!=-1) { if (s[p].next[i]!=-1) { s[ind].fall=s[p].next[i]; break; } p=s[p].fall; } if (p==-1) { s[ind].fall=root; } } q.push(ind); } } }}int main(){// freopen("test.txt","r",stdin); int T; scanf("%d",&T); while(T--) { preprocess(); int n; scanf("%d",&n); gets(a); while (n--) { gets(a); insert(); } gets(a); KMP(); printf("%d\n",find()); } return 0;} |
 评论 (0)
评论 (0)