给定一个无向图G，求它生成树的个数t(G)。
O(3n*n2) :dp
O(n3)：Matrix-Tree定理(Kirchhoff矩阵-树定理):
G的所有不同的生成树的个数等于其Kirchhoff矩阵C[G]任何一个n-1阶主子式的行列式的绝对值。
计算行列式的时间复杂度为O(n3)，因此，生成树的计数也可以在O(n3)的时间内完成。
证明的关键:
(Binet-Cauchy公式) 设A和B各为p*q及q*p矩阵，则有
特别的，detAAT=(detA)2。
Binet-Cauchy公式展开式中的每一项对应着边集一个大小为n-1的子集。
其中，值为1的项对应一颗生成树，而没有对应生成树的项值为0。
这样，将问题转化为求展开式中所有项之和。
模板题 ：【SPOJ104】Highways
计算基尔霍夫矩阵（拉普拉斯矩阵）L：
L=D-A
D：度矩阵当i≠j时,dij=0；当i=j时，dij等于vi的度数
A：邻接矩阵如果vi、vj之间有边直接相连，则aij=1，否则为0
1 2 3 4 5 6 7 8 9 10 | double D[N][N],A[N][N],L[N][N],deg[N];F(i,1,m){ int x,y; x=read();y=read(); A[x][y]=A[y][x]=1; deg[x]++;deg[y]++;}F(i,1,n) F(j,1,n) D[i][i]=deg[i];F(i,1,n) F(j,1,n) L[i][j]=D[i][j]-A[i][j];ans=Gauss(L); |
高斯消元求行列式：
注意：1\主子式2\绝对值
默认去掉第n行第n列, 消成上三角矩阵
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | inline double Gauss(double a[][N]){ double ans=1; int t=1; for(int i=1;i<n;i++){//【枚举当前行 int r=i; for(int j=i+1;j<n;j++)//【枚举下面的行 if(abs(a[j][i])>abs(a[r][i])) r=j;//r记录第i列最大值 if(r!=i){ t=-t;//行列式性质 for(int j=1;j<=n;j++) swap(a[r][j],a[i][j]);//两行所有数调换 } //与第i+1~n-1行所有数进行消元(均消为0) for(int k=i+1;k<n;k++){ double p=1.0*a[k][i]/a[i][i];////a[k][i]-a[k][i]/(a[i][i]*a[i][i])=0 for(int j=i;j<n;j++) a[k][j]-=p*a[i][j];//第二重循环枚举该行数字 } } //与高斯消元不同：不合并,而是对角线相乘 for(int i=1;i<n;i++) ans*=a[i][i]; return ans*t;} |
[当前求行列式的模板可能还不完善]
给出一个简单无向加权图，求图中不同的最小生成树个数。（如果两棵最小生成树中至少有一条边不同，则这两个最小生成树就是不同的）。
模板题：[JSOI2008]最小生成树计数
输出方案数对31011的模
最小生成树的两个性质：
1、边权相等的边的个数一定。
2、做完边权为w的所有边时，图的连通性相同。
挖坑：http://www.cnblogs.com/Tunix/p/4415971.html
用三种颜色给每条边染色，给出特定的边可染的颜色，
求不同染色方案的生成树数量
这个有点难...证明要用拉格朗日插值&%#￥...
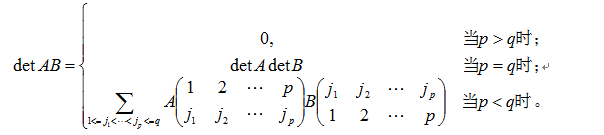
评论 (0)
