并查集是用树结构实现的。
①数组模拟指针
②根节点代表集合,初始时根节点指向自身
设树高为H。
查找操作:O(H)
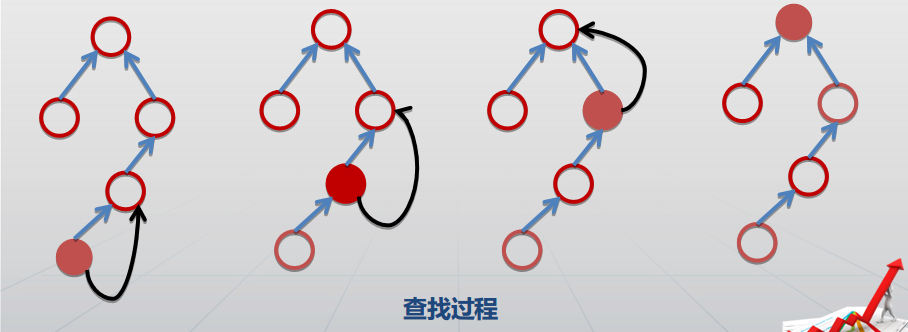
注意上图(好大>_<),实现就很好理解:
int find(int x)
{
while (father[x] != x) x = father[x];
return x;
}
int find(int x)
{
if (father[x] != x) return find(father[x]);
else return x;
}
合并操作:由②知树的合并操作对象为根节点,由①知合并就是改变根节点的指针指向。O(H)
void unionn(int x,int y)
{
x = find(x);y = find(y);
father[y] = x;
}
均摊:H=log2n
极端:H=n ==>相当于一个一个节点暴力合并!!递归写法有爆栈可能!!
我们受到了启发!
——于是接下来的优化操作被统称为“启发式策略”0.0!
优化的目的是减小树高.树越扁平,查找find(x)效率越高.
1、按秩合并
2、路径压缩
find(x)时进行.
int find (int x)
{
if (father[x] != x) father[x] = find (father[x]);
return father[x];
}
只要在回溯时增加一个赋值操作即可!
看看效果:
n个元素的m次不相交集合操作
◆按秩合并:时间:O(m*lg(n))
◆路径压缩:最坏:O(n+lg(n))
◆按秩合并和路径压缩: O(mα(n))
每次查找近似常数时间的复杂度!
终于明白为什么说并查集"实现简单,效果拔群"了,之前一直不太明白路径压缩的代码是什么玩意..你们一定以为我是普及组选手...(TuT)
 评论 (0)
评论 (0)