筛素数:预处理出1~n中的素数表,查询时可O(1)
暴力判断:依次判断1~n每个数是不是质数 O(n√n)
埃氏筛法:
复杂度证明:厄拉多塞筛法找到k的时候需要标记O(N/k)个数为合数。因此一共需要标记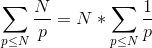 次,
次,
其中p <= N表示所有小于等于N的素数。这就是N乘以小于等于N的素数的倒数之和。右手边是O(N)*O(loglogN) = O(NloglogN)的。
代码:
线性筛法:
过程:
•设数组d记录[2,n]内的每个数的最小质因子,一开始全部置为0。
•从2开始依次检查d。若d[i]值为0,则i是素数,将其存入一个集合,并将d[i]设为i。
•之后,无论i是不是素数,都要遍历素数集合中不大于d[i]的素数p,将d[p*i]的值设成p。
•最后素数集合中的数就是[2,n]内的素数。
复杂度证明:对于每个合数,它只会被它的最小素因子筛一遍。也就是d的每个元素最多访问一次。
因此这个算法的时间复杂度是线性的O(n)。
代码:
POJ 2689
#include<iostream>
#include<cstring>
#include<queue>
#include<cstdio>
#include<cmath>
#include<algorithm>
#define N 100005
#define inf 1<<30
#define MOD 9973
#define LL long long
#define eps 1e-7
#define zero(a) fabs(a)<eps
#define equal(a,b) zero(a-b)
using namespace std;
bool flag[100005];
int prime[100005],cnt=0;
//先打出sqrt(上界)的素数表
void Prime(){
for(int i=2;i<=47000;i++){
if(flag[i])
continue;
prime[cnt++]=i;
for(int j=2;j*i<=47000;j++)
flag[i*j]=true;
}
}
bool isprime[1000005];
int a[1000005],c;
int main(){
int l,r;
Prime();
while(scanf("%d%d",&l,&r)!=EOF){
memset(isprime,true,sizeof(isprime));
if(l==1) l=2;
//利用之前的素数,进行二次筛选,注意防溢出
for(int i=0;i<cnt&&(LL)prime[i]*prime[i]<=r;i++){
int s=l/prime[i]+(l%prime[i]>0);
if(s==1)
s=2;
//不能从1开始,不然就把素数给判成合数了
for(int j=s;(LL)j*prime[i]<=r;j++)
if((LL)j*prime[i]>=l)
isprime[j*prime[i]-l]=false;
}
c=0;
for(int i=0;i<=r-l;i++)
if(isprime[i])
a[c++]=i+l;
//少于两个素数
if(c<2){
puts("There are no adjacent primes.");
continue;
}
int x1=0,x2=0,y1=0,y2=inf;
for(int i=1;i<c;i++){
if(a[i]-a[i-1]>x2-x1){
x1=a[i-1];
x2=a[i];
}
if(a[i]-a[i-1]<y2-y1){
y1=a[i-1];
y2=a[i];
}
}
printf("%d,%d are closest, %d,%d are most distant.\n",y1,y2,x1,x2);
}
return 0;
}
 评论 (0)
评论 (0)